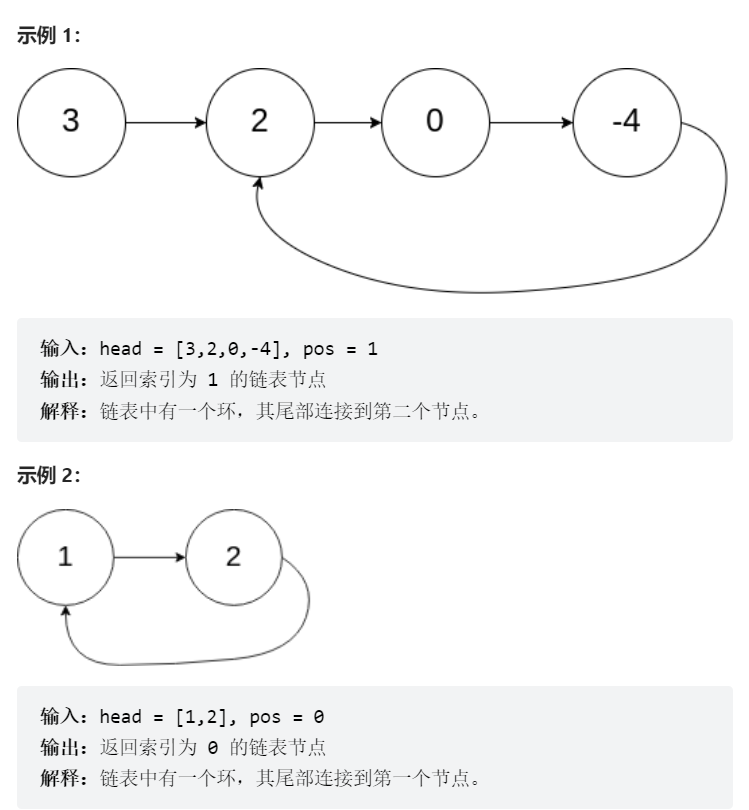
142.环形链表II

发表于 2022-09-06 分类于 LeetCode之链表阅读次数：本文字数： 2.6k 阅读时长 ≈ 2 分钟

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

【题目】

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改链表。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/linked-list-cycle-ii

分析：

主要考察两知识点：

判断链表是否环

如果有环，如何找到这个环的入口

【解答】

1、快慢指针 - 常规方法

时间复杂度：O(n)

空间复杂度：O(1)

分两个步骤进行

①利用快慢指针判断链表是否存在环

这个道理就是一个人一步步跑，另一个人两步两步跑，最后第二个人超越了第一个人一圈，让然后相遇了。如果说不存在环的话，那么快指针会先跑到终点，指向nullptr

②利用双指针判断环的入口-这里涉及到数学推导

题目说明

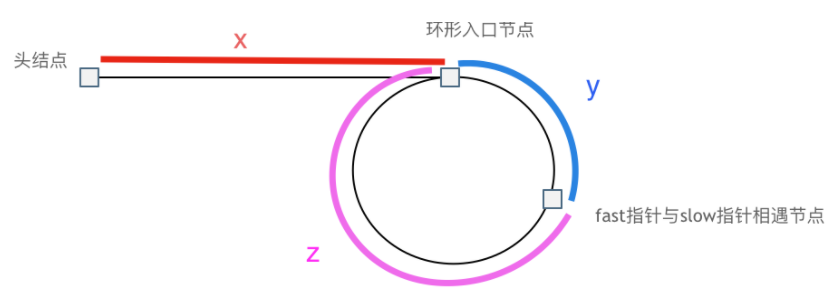
最终x = z ；x是我们想要去求解的量，在fast指针和slow指针相遇后，让fast指针一步步走。让slow从头节点开始一步步走，重合的时候就是结点所在的位置。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
    ListNode* slow = head;
    ListNode* fast = head;
    while (fast != nullptr && fast -> next !=nullptr) { 
      // 保证 fast -> next ;以及 fast -> next -> next 存在
      slow = slow -> next;
      fast = fast -> next -> next; //由于这里向后移动了两次，为了保证不会出现空指针指向空指针
      //判断条件那里需要格外小心
      if (fast == slow) {  // 两个节点相遇
        slow = head;
        while (slow != fast) {
        slow = slow -> next;
        fast = fast -> next;
        }
        return slow;
      }
    }
     return NULL;
   }
};

2、map/unordered_map - 常规方法

最基本的想法，创建一个键值表，如果出现了曾经出现过的节点就可以返回了。

时间复杂度：底层基于红黑树的map，在查找某个元素的时候，采用二分查找的办法，时间为O(lgn)；链表n个节点，时间复杂度O(nlgn). 反之，如果是无序的unordered_map，元素没有排序，所以时间复杂度为O(n)

空间复杂度：创建了一个哈希表 O（n）；

利用map 进行实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
     if (!head) { //如果链表是空的直接返回NULL
       return NULL;
     }
     map<ListNode*, int> key;  // 创建map
     ListNode* pcur = head;
     while (pcur) { //当指针不为空的时候就进行
     //先判断是否出现过当前的指针，出现了就直接返回
     if (key.find(pcur) != key.end()) { //发现当前指针对应的并不是map的末尾，说明出现过，那就是环
     return pcur;
     }
     //没出现就添加到map里面
     else {
       key[pcur] = key[pcur] + 1;
     }
     //指针向前移动
     pcur = pcur -> next;
     }
     return NULL; // 直到遍历完了 末尾空指针跳出了循环说明没有环出现
    }
};

3、野路子-非常规方法

时间复杂度O(n)

空间复杂度O(1)

链表是在堆上申请的空间，从低向高，如果是按顺序进行链表节点内存的申请，那么我们在环的那一点，一定存在 head → next 小于head；利用这个规律，复杂度为O（n），可以比较快速的解决问题。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
      while (head != nullptr) {
        if (!less<ListNode*>()(head,head->next)) // !(head地址小于head -> next)
        {
        return head -> next;
        }
        head = head -> next;
      }
      return NULL;    
    }
};